Loading... # Lec 5~6:实时环境贴图 Real-time Environment Mapping ## 0. 环境光照 [我的笔记3的5.1节](https://www.irimsky.top/archives/250/)  ## 1. 求解环境光照着色(分割近似求和法、IBL) 环境光照着色同样需要渲染方程,求解渲染方程需要蒙特卡洛积分,需要大量采样,更不用说求解环境光照是一整个圆球的范围。这样会让整个流程很慢,所以带有采样的着色器一般不适用于实时渲染。 我们观察一下镜面反射和漫反射的情况: - 左图的镜面反射,入射的光大部分集中在一小段范围内,所以进行蒙特卡洛积分时**积分域很小** - 右图的漫反射,几乎所有方向都是入射方向,但是漫反射的BRDF几乎是均等的,**函数光滑** 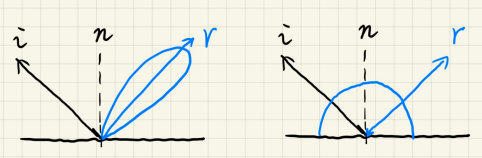 由此我们联想到了上篇所讲的一种约等式(**分割近似求和法**):(注意$\Omega_G$的变动) 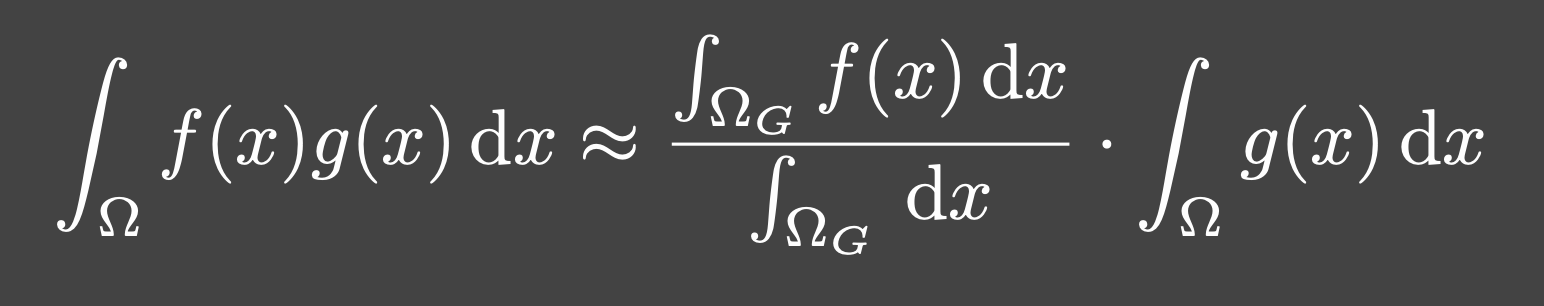 所以我们可以将渲染方程约等于: 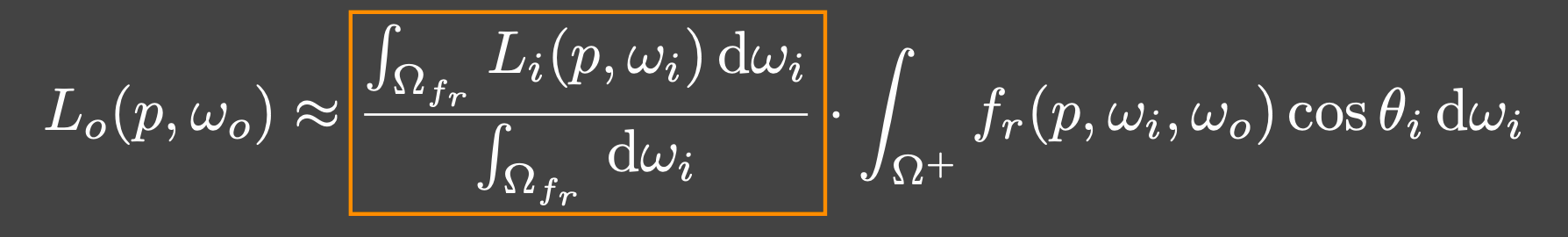 ### 1.1 预滤波环境贴图 观察图中的橙色方框内容,**对于环境光照**,它是可以被**预计算**得出的。它其实就是要计算某一区域(BRDF的积分域)内的光照总和的平均。所以很容易想到**预滤波环境光**。 但是对于不同粗糙度的表面,积分域大小不一样,粗糙的表面积分域理应更大(反射范围更大)。像MipMap一样,我们将其按照**不同的粗糙度**进行滤波,根据BRDF的积分域大小来选取某一粗糙程度层级的滤波结果。(在两个层级间可以三线性插值)  接着只要在对应的环境光照贴图上取反射方向的**那一点**即可,因为是已经经过滤波的结果,所以就相当于原图的平均值 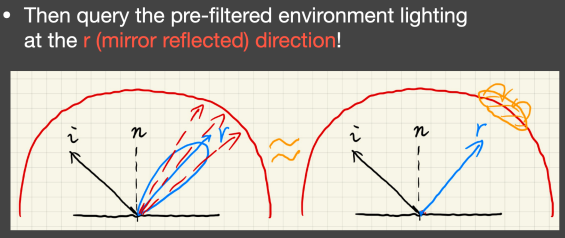 ### 1.2 BRDF部分 接着我们要想办法消除后半部分的积分:  回忆一下微表面理论 ([参考GAMES101笔记8的1.4节](https://www.irimsky.top/archives/289/)): 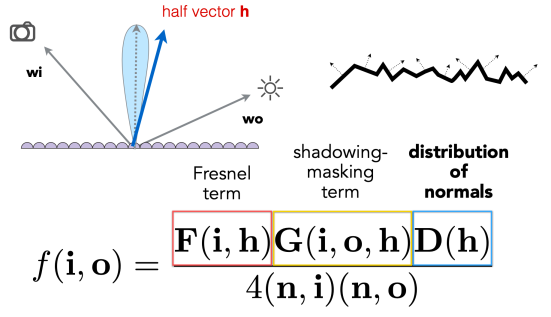 如果仍然要进行预计算的话,需要考虑到所有的因素的组合(菲涅尔项,粗糙度等等..)维度将会很高,存储开销很大。所以需要想出其他办法。 我们有近似描述菲涅尔项的方法: **Schlick近似**($R_0$ 是基础的反射率,$\theta$ 是入射角度) 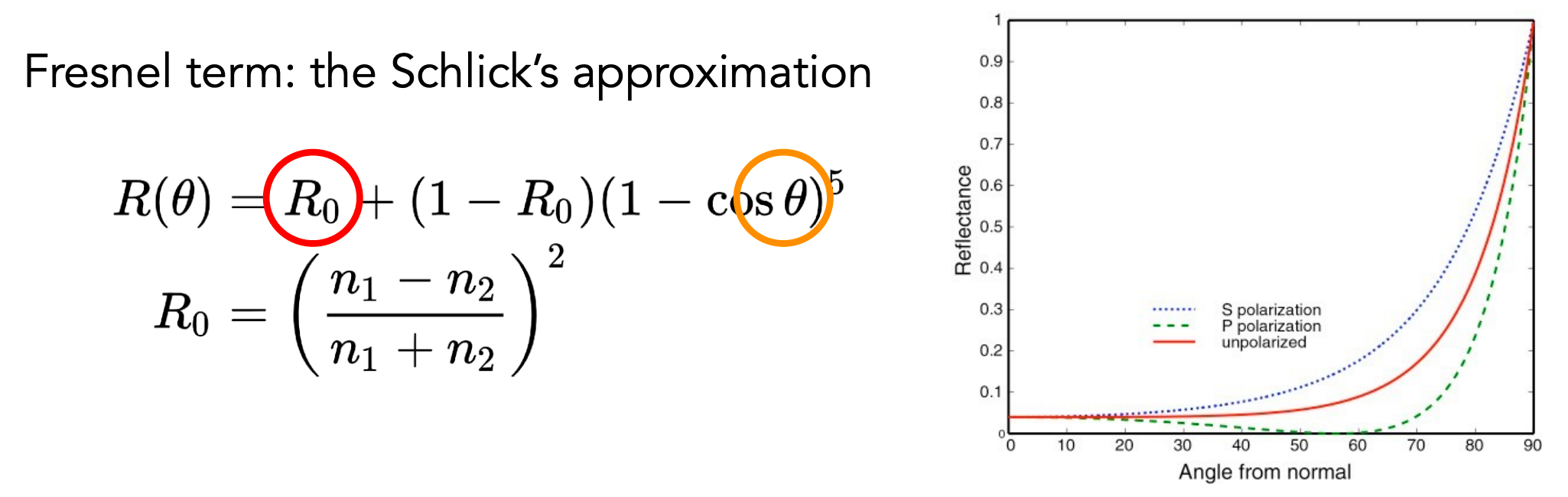 描述**法线分布函数(NDF,$D(h)$)**的一个方法:**Beckmann分布**。 其中的$\alpha$可以用于定义roughness,$\alpha$的值越高,分布函数的整体就越低,意味着表面更粗糙,漫反射成分越大,反射出来的光就越少。 $\theta_{h}$是半程向量与法向量的夹角,这个可以转化成入射角度,所以和上述的 $\theta$ 视作是同一个变量  综上所述,维度便通过近似,减少到了3个维度: $\alpha$(roughness)、$\theta$(入射角度,可以和半程角度、出射角度互相转化)、$R_0$(基础反射率) 但是我们还可以简化: 将Schlick近似公式代入的菲涅尔项,得到: 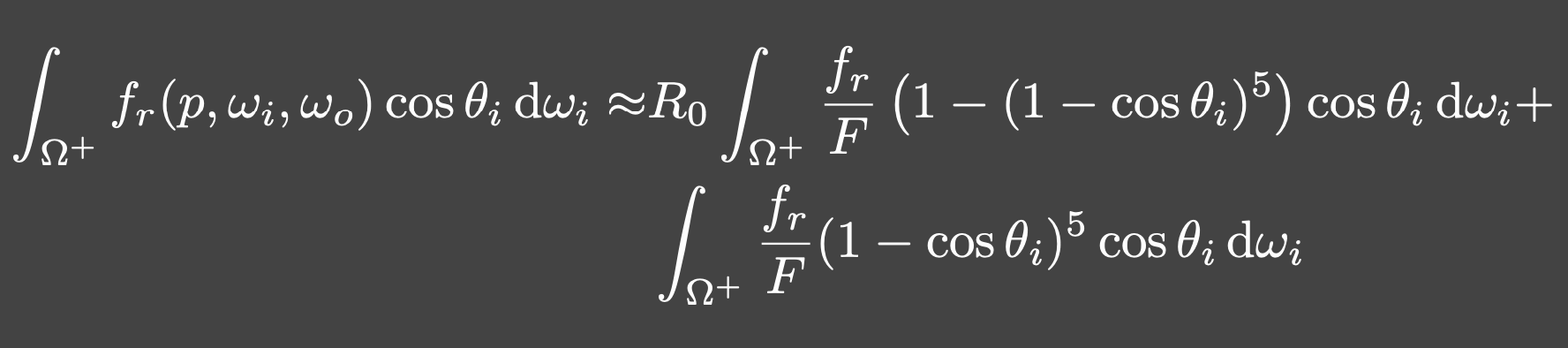 这下就可以将$R_0$提取到积分外部了,而 $\frac{f_r}{F}$ 中已经不剩菲涅尔项,只剩下G、D项,所以整个公式只剩下$\alpha、\theta$ 两个变量 由此我们就可以使用预计算了: 以 roughness、$\cos\theta_i$ (范围0~1,方便)为坐标轴,存储一张预计算二维表格,自然而然就想到了使用纹理来存储。两个部分分别存在两个通道即可:  这样,就完全避免了采样,可以很快地获得一个很真实的结果:  但是工业界一般不用积分,而是用离散求和来替代: 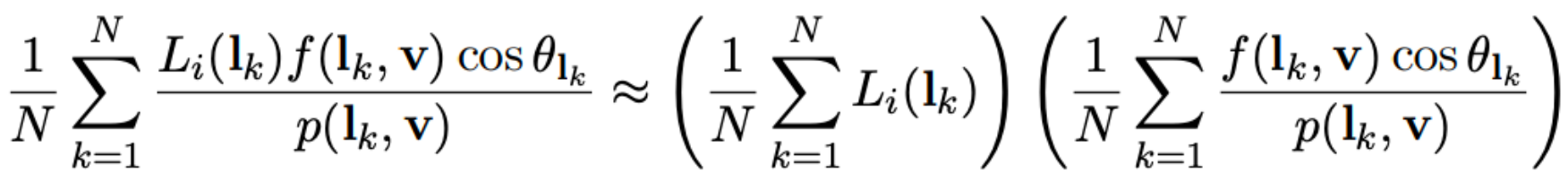 其中$l_k$是入射光线,$v$是交点, $p(l_k, v)$是概率密度函数,指$v$点接受的光线会从$l_k$方向来的概率,参考 [蒙特卡洛积分](https://www.irimsky.top/archives/277/) 所以这个方法叫 “分割近似**求和**”,而不是“分割积分” 以上的方法称为 **Image-Based Light (IBL)**。讲的比较简单模糊,更详细的推导以及讲解可以参考: [【基于物理的渲染(PBR)白皮书】(一) 开篇:PBR核心知识体系总结与概览](https://zhuanlan.zhihu.com/p/53086060) [深入理解 PBR/基于图像照明 (IBL)](https://zhuanlan.zhihu.com/p/66518450) [DX12渲染管线(1) - 基于物理的渲染(PBR)](https://zhuanlan.zhihu.com/p/61962884) [LearnOpenGL:IBL](https://learnopengl-cn.github.io/07%20PBR/03%20IBL/01%20Diffuse%20irradiance/) ## 2. 环境光照阴影 实时渲染中的环境光阴影是一个很难解决的问题:光源很多、范围很大。业界一般只会处理一个典型的光源:太阳。 ### 2.1 Precomputed Radiance Transfer (PRT) #### 2.1.1 球谐函数 Sphere Harmonics 球谐函数是一系列定义在**球面上**的**二维**的**基函数**$B_i(\omega)$,表示一个方向(球面上 $\theta、\phi$ 就能表示所有方向 $\omega$) 类比傅里叶变换,可以将任意**二维函数**表示成球谐函数基函数的组合,而且可以实现不同的频率 对于函数$f(\omega)$, 求出球谐函数基函数的系数的过程,如下图所示,积分的解法一般是采样。这一过程叫做 **投影**,(类比坐标轴投影)  下图是球谐函数的可视化,$l$ 越大变化频率越大。 同一个$l$阶下的基函数都是正交的,一般选取的前 $l$ 阶全都用来表示原函数。 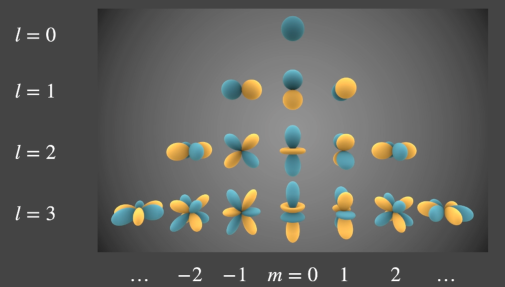 最早引入球谐函数是用于着色的:  可以看出,仅仅**前3阶基函数就可以很好的描述一个漫反射**的着色了(这也是当时引入的论文得出的结论),因为漫反射的BRDF就是一个低频函数,$\int BRDF×L_i$ 也会是一个低频函数(卷积的性质) #### 2.1.2 求解阴影 对于一个着色点求解环境光照的渲染方程(因为要计算阴影,所以要考虑visibility),我们要用到这些数据: 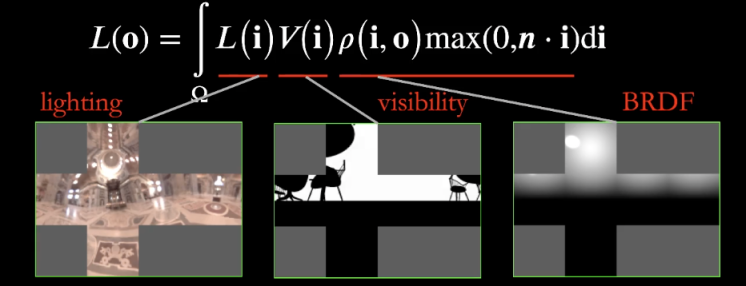 假设环境贴图分辨率是6×64×64,那么每一个着色点都要进行6×64×64的采样计算,这样的开销是非常大的。 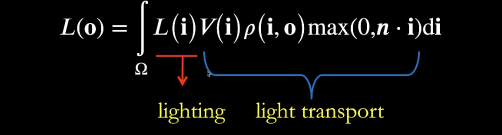 我们可以将渲染方程视作两个部分:光线部分与光线传输部分。 现在我们假设**场景不会变动**,那么**光线传输部分不会发生变化**。所以变动的只有光线部分。对于不会变动的部分,我们很容易想到**预计算**。而对于光线部分,因为它的范围是一个球面(半球),所以我们可以用**球谐函数**将其拆分成基函数表示。 - 先用**漫反射项**解释怎么预计算: 漫反射的BRDF是个常数,将其提出积分外。将$L(i)$拆分成$\sum{l_iB_i(i)}$ 代入渲染,$l_i$是基函数系数,一个常数,提出积分。积分中剩余的项就是可以预计算的部分,只含有入射方向一个变量(相当于再做一次球谐函数的投影)。  然后将预计算项设为$T_i$ ,那么就可以发现,渲染方程变成了一个点乘的形式(球谐函数的系数 dot 预计算项)。 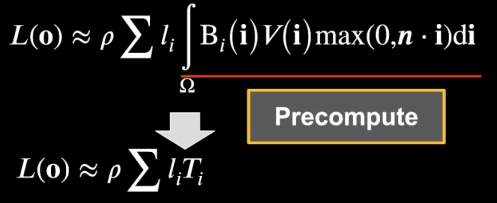 利用球谐函数的性质,我们允许光源进行简单的旋转。旋转之后的系数变更可以很快求出。光源的切换也是可以的,只要换一套预计算的$l_i$即可 - 接下来讲解 **glossy项(光滑项)**: 因为光滑项是无法变成常数然后提取出积分的,所以预计算的项还需要考虑出射方向$o$: 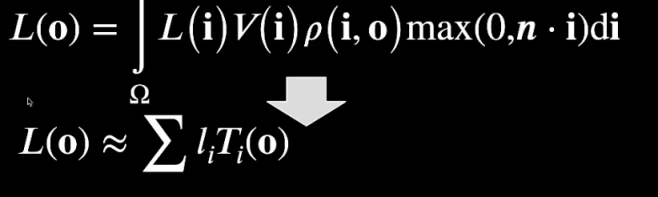 注意到以出射方向为变量的函数其实就是个球面函数,那么将 $T_i(o)$ 再次用球谐函数分解: 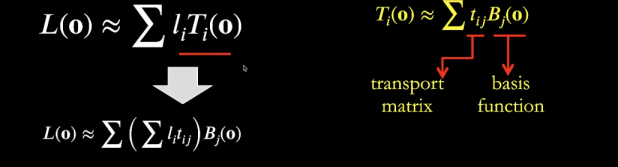 !!!!看原论文:[https://jankautz.com/publications/prtSIG02.pdf](https://jankautz.com/publications/prtSIG02.pdf) $\sum l_i t_{ij}$部分是肯定可以预计算了。 原论文中提到,这个算法为了保持化简效果,要么**固定光源**,要么**固定视角**。如果固定光源的话,视角可以变动,不过每次都要重新计算基函数$B_j(o)$,然后进行一次点乘;而固定视角,可以直接把基函数$B_j(o)$也预计算出,每次只需要一次点乘。 这样,光线传输的部分的预计算量就变成了一个矩阵。同样这也提升了存储的开销。  实际应用中通常只用3阶的基函数描述。对于真正的完全镜面反射(频率很高)球谐函数的表现并不太好,所以不会采用PRT方法。 > 把辐射率的传输(包括阴影和相互反射的关系)预生成球谐函数SH的系数,存储在几张纹理中(SH lightmap)。然后,存储静态 light probe 的 SH,或动态地把光源生成 SH,点积后就可以得到含有环境光照、阴影和相互反射的全局光照效果。不过系数有限,光照结果是低频的。Halo 3 有使用 [3]。 #### 2.1.3 考虑多次弹射 顺着上节的结果分析,我们将渲染方程分成了光线部分和光线传输部分。如果要考虑多次弹射,其实只是**将光线传输部分重复多次**,修改预计算的规则即可,变复杂的只有预计算,并没有让实际渲染变慢。 而且预计算阶段不用考虑性能的问题,可以用各种方法,比如光线追踪等,最后将计算得到的系数存储下来即可。   当然PRT方法有很多**局限性**,比如说描述高频效果并不好(为了还原高频信息需要很高阶的基函数),以及场景不能动的限制,巨大的存储开销等等。 > 摘自本篇作业总结 > > 物体在不同光照下的表现不同,PRT(Precomputed Radiance Transfer) 是一 个计算物体在不同光照下表现的方法。光线在一个环境中,会经历反射,折射, 散射,甚至还会物体的内部进行散射。为了模拟具有真实感的渲染结果,传统的 Path Tracing 方法需要考虑来自各个方向的光线、所有可能的传播形式并且收敛,速度极慢。PRT 通过一种预计算方法,该方法在离线渲染的 Path Tracing 工具链 中预计算 lighting 以及 light transport 并将它们用球谐函数拟合后储存系数,这样就将时间开销转移到了离线中。最后通过使用这些预计算好的数据,我们可以轻松达到实时渲染严苛的时间要求,同时渲染结果可以呈现出全局光照的效果。 最后修改:2022 年 03 月 24 日 11 : 15 PM © 允许规范转载