Loading... # Lec 07~09:Shading 着色 在图形学中给不同的物体应用不同的**材质**(material)这一过程,叫做**着色(Shading)** ## 1. Blinn-Phong 光照模型 Blinn-Phong是一种简单的光照模型,它的主要结构由3个分量组成:**环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照**。  - **环境光照**(Ambient Lighting):上图中,有些部分是背光面但是仍然有颜色,因为其接受了各种间接光照。 来自环境的反射光很复杂,为了模拟这个,我们会使用一个环境光照常量,它永远会给物体一些颜色。 - **漫反射光照**(Diffuse Lighting):模拟光源对物体的方向性影响(Directional Impact)。 它是Blinn-Phong光照模型中视觉上最显著的分量。物体的某一部分越是正对着光源,它就会越亮。 - **镜面光照**(Specular Lighting):模拟有光泽物体上面出现的高光处。 镜面光照的颜色相比于物体的颜色会更倾向于光的颜色。 > https://blog.csdn.net/weixin_43803133/article/details/107616245 在继续之前,先定义一些东西: 计算一个特定的着色点对于相机的光照反射 输入(以下都是单位向量): - 观测方向:$\vec{v}$ - 表面法向量:$\vec{n}$ - 光照方向:$\vec{l}$ - 表面参数:颜色,亮度等 ### 1.1 Diffuse Lighting 漫反射光照 光线被散射到各个方向上,表面的颜色从任何角度观测都是一样的。  但是有多少光线能量是被接收的?根据**Lambert余弦定律**可得:每个单位面积接收的光与 光照方向 $l$ 与表面法向量 $n$ 的夹角的余弦 成正比  同时,光的能量会随着距离衰减。我们假设光来自于一个点光源,点光源无时无刻不散发出能量,我们可以以球形的方式来看光能量的衰减。在某时刻发出的光能量,在扩散的过程中,随着扩散的距离变小,也就是因为变成球壳的表面积变大了,所以能量在单位点上就变得越来越稀疏了。  所以,**Lambert漫反射着色公式**如下:  其中, $\max(0,\vec{n}·\vec{l})$ 则是为了防止负数的情况(即从表面底部入射) $k_d$表示漫反射系数,取决于这个着色点的颜色,会吸收多少能量。 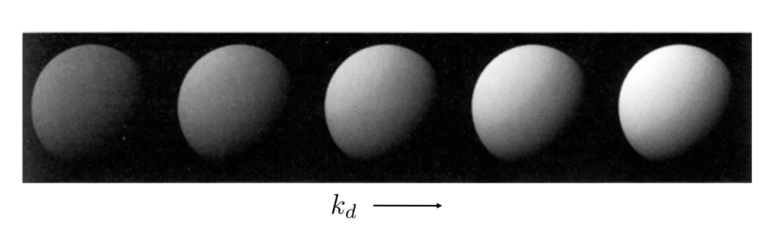 ### 1.2 Specular Lighting 镜面反射光照 比较光滑的物体表面通常符合镜面反射的特性:入射角等于反射角。只有观察的方向和镜面反射的方向才能看到物体表面的高光。 Blinn-Phong对于镜面反射的处理是: - 取光照方向 $\vec{l}$ 与 观测方向 $\vec{v}$ 的单位半程向量 $\vec{h}$(夹角中线) - 根据 $\vec{h}$ 与 法向量 $\vec{n}$ 的夹角的余弦值,作为衡量**观测方向与镜面反射方向的接近值** 所以镜面反射光强公式如下:  注意其中 $\max{(0,\vec{n}·\vec{h})}^{p}$有一个指数$p$ , 这是因为余弦值虽然可以体现两个向量之间的接近值,但是其“容忍度”过于高。比如在下图1中,在45度时余弦值仍然有些偏大,这不符合常理中的镜面反射情况。所以在余弦值加上一个指数可以有效 “加速余弦值的下降速度”。  所以这个$p$ 值可以用于**控制高光面大小**。如下图所示,随着$p$ 的增大,高光面越来越小,因为对其“接近值”的要求越来越高。  ### 1.3 Ambient Lighting 环境光 来自环境的反射光很复杂,为了模拟这个,我们会简单地使用一个**环境光照常量**,它永远会给物体一些颜色。所以这只是一个近似的模拟。 环境光照公式如下: 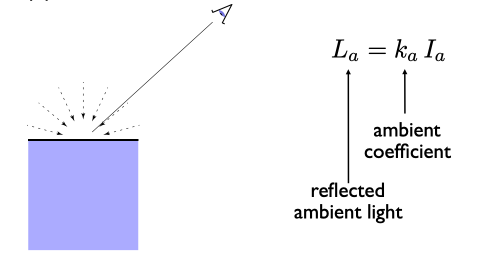 ### 1.4 结合成Blinn-Phong 将三者结合就得到了Blinn-Phong光照模型  ## 2. 着色频率  上图三个球体,从边界的锯齿可以看出,它们用的是同一个模型框架,但是它们的表面看起来不一样。 造成这一差异的原因就是**着色频率**(Shading Frequency),即着色应当应用于哪一点上。 图一是对平面做着色,图二是对每个顶点做着色,图三则是对每个像素做着色 ### 2.1 对平面着色 flat shading 通过三角形的边求出**整个三角形**的法线,然后把它当作一个点进行着色。**并不适用于平滑表面**。  ### 2.2 对顶点着色 Gouraud shading 求出三角形**三个顶点**各自的法线,在每个顶点上进行着色,然后在三角形内部做一个**插值**。  ### 2.3 对像素着色 Phong shading 通过三角形的三个顶点的法线信息,然后在三角形内部**每个像素**都可以插值出一个独特的法线方向,然后逐个进行着色。  ### 2.4 对比 并不一定Phong就优于另外两个,**模型面数越高他们的差距越小**;同时**Phong的开销更大**。  ### 2.5 顶点法线 一个顶点的法线的求法: **取其相邻的平面的法向量的加权平均值** 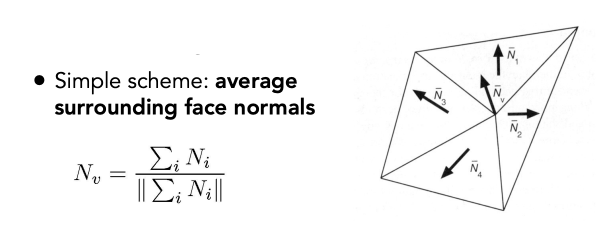 记得法线都要**归一化** ## 3. 图形管线 图形渲染管线是实时渲染的核心组件。渲染管线的功能是通过给定虚拟相机、3D场景物体以及光源等场景要素来产生或者渲染一副2D的图像。 从一个3维场景得到到一张图的过程: - 定义顶点 - 定义顶点连成三角形面 - 光栅化:采样,深度测试等 - 对片元 (fragment) 处理 - 得到输出的帧  在这其中,**Vertex Processing** 和 **Fragment Processing** 这两个过程是允许我们自定义编程shader的,分别对应 **顶点着色器** 和 **片段/片元/像素着色器** ## 4. 纹理映射 在给三维物体的表面进行着色的时候,我们希望他表面的色彩变化更多,我们把想要的颜色储存在一张图上,然后把三维物体的表面给展开成二维平面,然后使得图上的点和三位表面的点对应起来。这一展开的过程就叫做 **uv展开**。 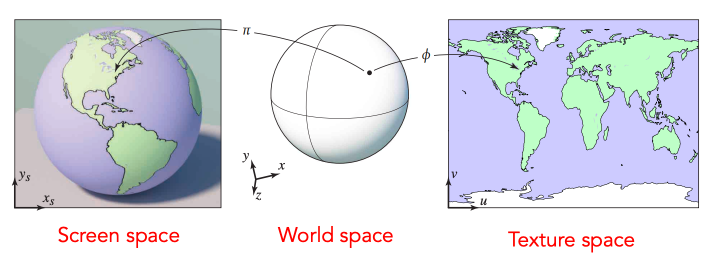  通常会将纹理展开后,其中的坐标称为 **(u,v)**,u、v的范围都是(0,1),不论长宽比是多少。 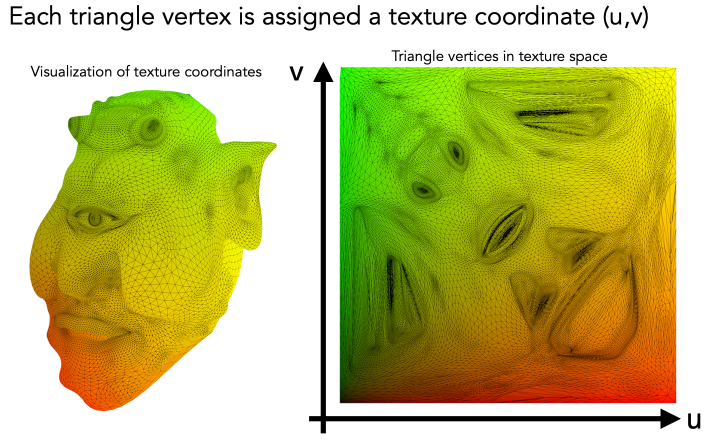 不同的位置可以用同一个纹理,比如下图中的墙砖,他们其实都是同一个纹理拼接而成。 可以注意到,在拼接的边缘处做到了无缝衔接,这是纹理设计的妙处,使其从四个方向上拼接自己都可以做到无缝拼接。   ### 4.1 重心坐标 我们有很多操作需要在三角形的顶点上进行,同时在三角形的内部进行一个平滑的“过渡”,即**插值**。 为了做到这一点我们需要引入重心坐标。 重心坐标是定义在三角形内部的,对于三角形ABC内部任意一个点$(x,y)$我们都可以将它写成$\alpha A+\beta B+\gamma C$ 的形式,其中 $\alpha +\beta +\gamma = 1$ 且都为正数。 所以,三角形内部的点可以直接用 $\alpha,\ \beta,\ \gamma$表示,此即为**重心坐标**。  可以利用某个点划分的面积算出该点的 $\alpha,\ \beta,\ \gamma$ 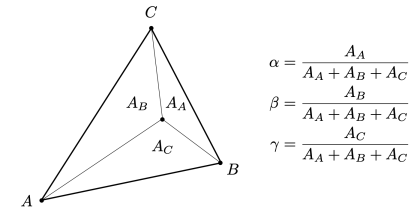 若 $\alpha = \beta = \gamma = \frac{1}{3}$,则这个点即为**三角形的重心**。 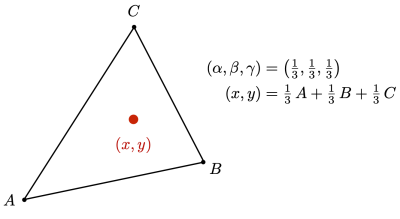 利用叉积的性质,可以根据某点具体的坐标$(x,y)$ 计算出它的 $\alpha,\ \beta,\ \gamma$  有了 $\alpha,\ \beta,\ \gamma$ ,即可利用其进行线性插值,如下图所示。其中的 $V$ 可以是各种各样的属性值,比如深度、颜色、纹理坐标、法线等等。  - 注意:投影过后的原本三维空间中的重心坐标将会失去意义,原本的重心坐标已经不是新的重心坐标了。所以有一些属性只能在三维空间中做的我们就必须在投影之前做,或者投影之后需要用到的时候再把坐标投影回三维空间应用三维空间中的插值,或者详见:[透视矫正插值](https://blog.csdn.net/qq_38065509/article/details/105878504) ### 4.2 使用纹理时的问题 一种简单的纹理映射方法:对于每一个光栅化屏幕上的采样点 $(x,y)$,我们使用(在原三维空间对应的)重心坐标计算出其对应的纹理坐标 $(u,v)$,将屏幕点$(x,y)$设置为纹理上的$(u,v)$坐标的颜色。(若纹理的 u, v 位置非像素中心则取最近像素) 但是这样简单的方法会导致很多问题。 #### 4.2.1 纹理过小 纹理本身分辨率太小的话,将其用于一个分辨率很高的屏幕上,很多个采样点会映射到同一个纹理像素上,会导致一小块范围内的颜色是一样的。 下图中的图一便是这样的一种走样。  图二的效果则是**双线性插值**的效果,而图三则是**双三次插值**。虽然得到的结果有些模糊,但是却有效解决了锯齿的问题。 下面讲一讲双线性插值,它能得到一个相当不错的结果,并且将开销控制在合理范围内。 如下图,虚线边框是一个4×4的纹理图,黑点表示纹理像素中心。现在想要求得红点所在的像素值,  我们选取四个离红点最近的像素点(这四个像素点的中心连接起来要可以包围该红点)。先计算红点上下两边的线性插值(图中的 $u_1,\ u_0$),再计算红点垂直方向上的线性插值。 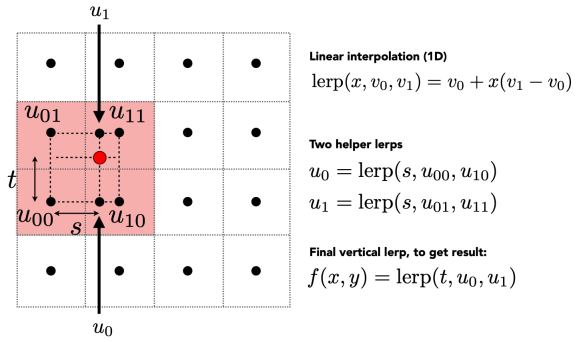 #### 4.2.2 纹理过大 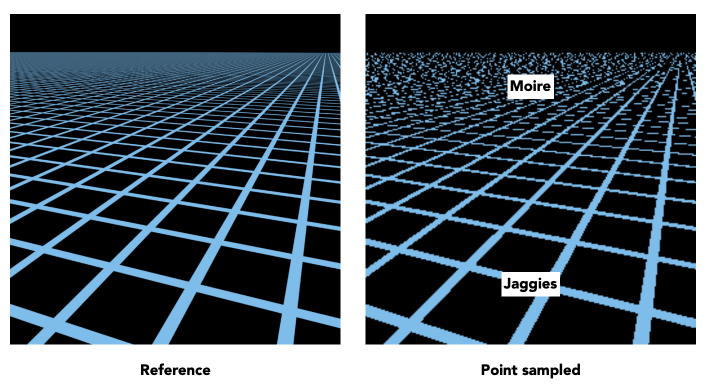 如上图所见,当纹理过大时,会出现走样现象。这是因为不同地方的像素覆盖的纹理多少不同,越远的地方,一个像素所覆盖的纹理就越多。采样的频率显然不足以描述纹理变化的频率。 下图背景是光栅屏幕,蓝色方框表示纹理的一个像素,越向左,这种现象越严重:一个采样点内的纹理像素过多,必然导致贴图的走样 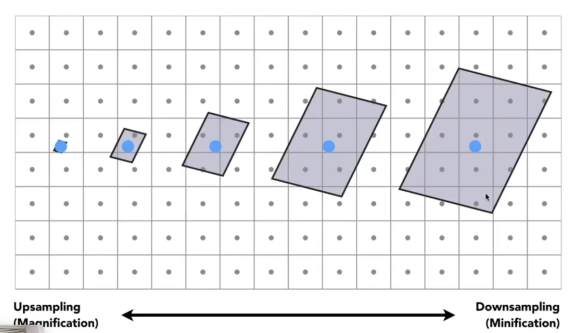 虽然使用超采样可以解决问题,而且会得到一个不错的结果,但是这样的性能开销过大。 这里可以尝试另一种思路,**不进行采样,只需获取范围内的像素平均值即可。** 图形学通常是使用**Mipmap**方法获取这个平均值。Mipmap方法是通过一张图预处理生成若干张图,每张图的分辨率递减。它的特点是:快,近似,**只能用于正方形**。  这里我们将原始图片当做第0层,实际上后面7层图片加起来所占的大小只有原图的1/3,并没有特别多的存储开销  那么要如何知道光栅化的某个像素点对应了多大的纹理呢?可以用一个简单的近似方法: 将所需要的像素点与相邻的像素点在纹理图上的坐标都求出来,比如下图中,将右方(10)与上方(01)的像素点都求出,用该像素点(00)在纹理上的坐标 到 10/01在纹理上的坐标 的距离的最大值 $L$ 作为一个**近似**的结果,即00像素点在纹理上覆盖的区域的边长。 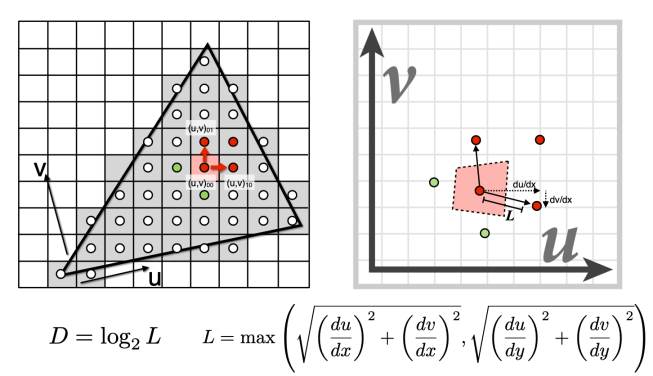 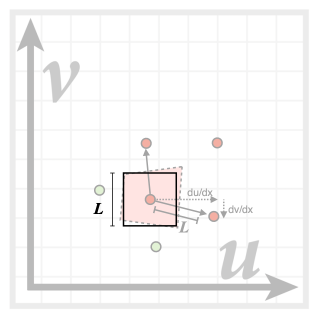 之后就可以简单地用$D=\log_{2}{L}$ 近似出最接近的Mipmap层数。 下图是将Mipmap层级在模型上可视化的图像。可以看出,离的近的窗台是红色,意思是我们需要看的比较细致的部分;而远处蓝色的墙壁则是表示层级较高的部分。  但是我们也看到了,有些连续地方的层级是不一样的、交错的,因为在计算层级$D$的时候只是离散地四舍五入取近似了。为了达到平缓地“过渡”,我们仍然需要插值。 对于这种情况我们可以用 “**三线性插值**”,其实就是在求纹理颜色的双线性插值的基础上再根据所求的 $D$ 进行一次线性插值。 比如对于求得 $D=2.6$ 的像素,我们分别计算它在 $D=2$ 与 $D=3$ 的双线性插值的结果,然后再分别用0.4 和 0.6 (2.6的小数部分)做系数,再进行一次线性插值。  下图即为三线性过滤后的结果  当然Mipmap并不是万能的。Mipmap会把远处的细节都模糊掉,比如下图。因为它只能查询**正方形**方块的区域内,以及插值毕竟只是近似。  另一种方法叫 **各向异性过滤** 可以有效解决这个问题。在此不进行细讲。 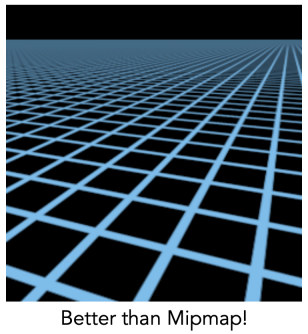 ## 5. 纹理的应用  在现代GPU当中,纹理一般用于记录**用于片元着色的信息和范围查询**(滤波)。 ### 5.1 环境贴图 环境贴图可以描述环境光照。假设环境光无限远,只记录方向。 下图左图为来自环境的光,右图为映射在茶壶上的光照。  下图左图的球为来自环境的光,右图为用此环境光渲染的场景。(中间的球面反射的就是左图的环境光)  这样的“球体” 我们就引申出了一个概念:[球形环境映射](https://zhuanlan.zhihu.com/p/84494845)(Spherical Environment Map),将四周的环境光扭成一个球体来存储,类似于地球仪。  当然这个方法有个问题,类比地球仪上高纬度地区面积看起来缩小的问题,在顶部和底部的图像会被扭曲,比如下图。  为了解决这种问题,引申出了 立方体映射(Cube Map),将环境光记录在立方体的各个面上。因为立方体各个面都是均匀的,所以几乎没有扭曲,不过需要一些坐标转换的计算。   ### 5.2 凹凸贴图 凹凸贴图的纹理记录了高度移动,不改变模型原本的几何信息。贴图作出人为的假的法线,由此得到假的着色效果,产生凹凸效果。  通过自定义的高度差,逐像素地定义模型表面的法线方向;法线方向一改,着色结果就会发生变化 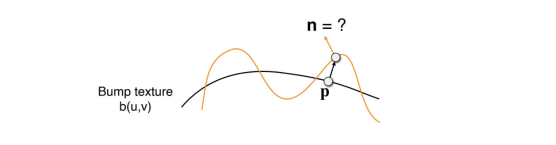 计算法线方法: 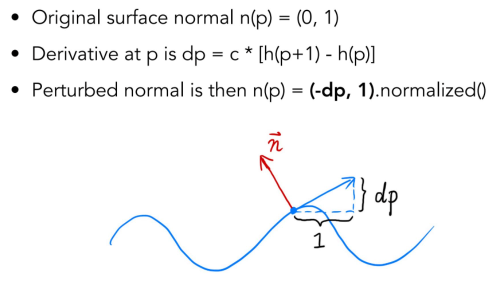  ### 5.3 位移贴图 位移贴图与凹凸贴图使用的是同一种贴图,但是相较于凹凸贴图,位移贴图是通过**移动顶点**来达到较为真实的凹凸的效果。 在边缘地方位移贴图比凹凸贴图更为真实。而且位移贴图是实际改变了模型的几何,所以凸起的地方会在自己身上留下阴影,而凹凸贴图则不会(下图可以看出)。 所以位移贴图要求模型的三角形足够细致,且运算量更高。 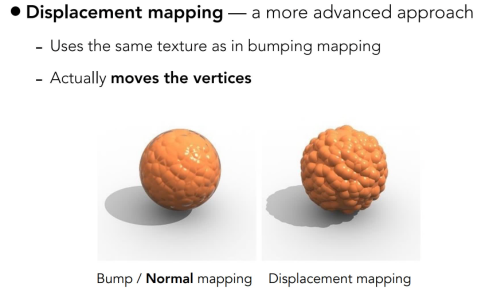 ### 5.4 预计算着色 物体表面的一些信息可以预先计算好,写进贴图中,然后再将纹理贴上。比如下图中的环境光遮蔽贴图。  最后修改:2021 年 11 月 25 日 04 : 37 PM © 允许规范转载